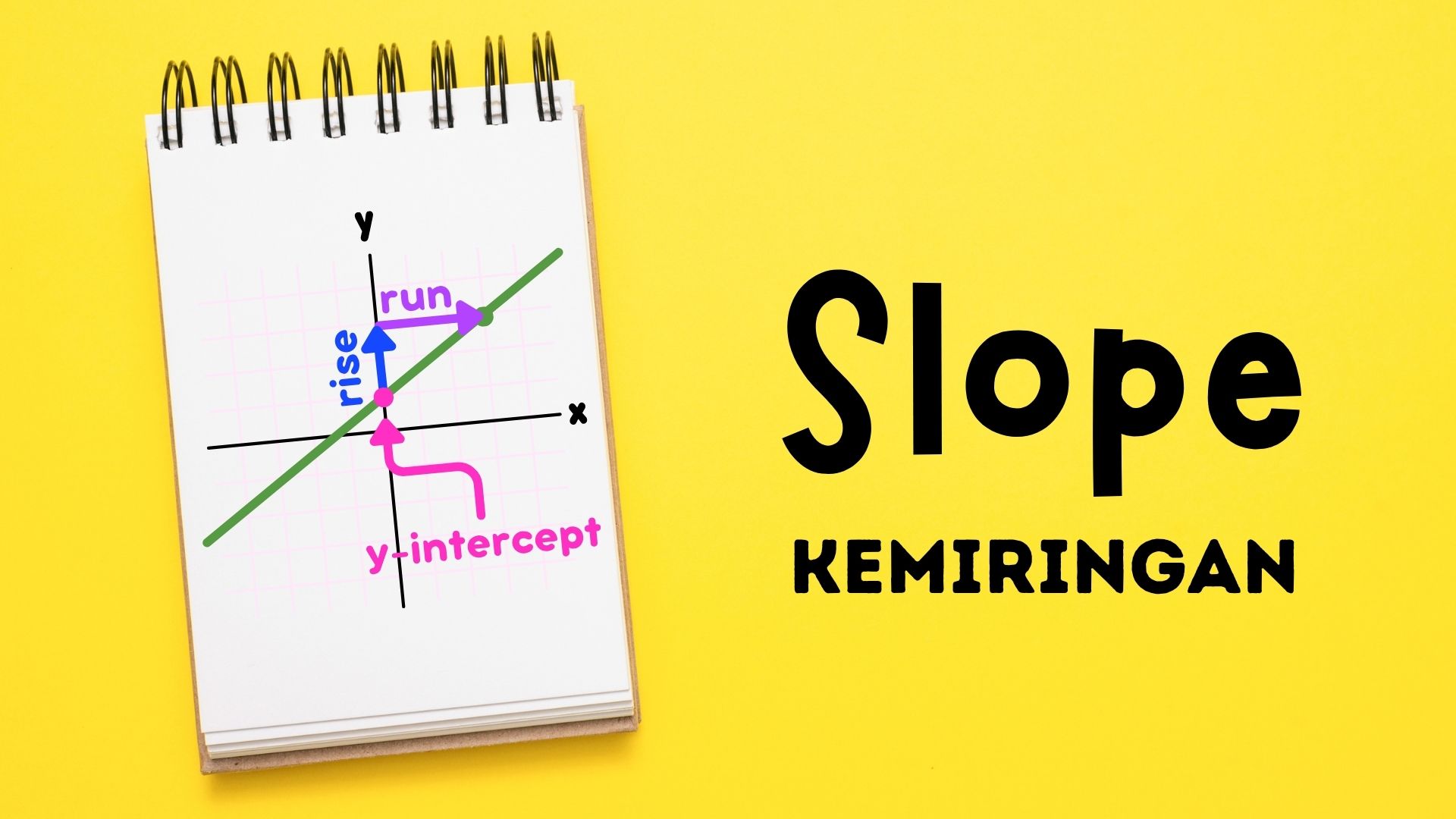
Dasar-Dasar Aljabar: Memahami Konsep Kemiringan (Slope) Garis

Dalam aljabar dan geometri analitik, kemiringan (atau slope/gradien) adalah konsep fundamental yang mendeskripsikan kecuraman dan arah sebuah garis lurus. Ini adalah alat ukur sederhana namun sangat kuat yang memberi tahu kita seberapa cepat suatu variabel berubah terhadap variabel lainnya.

Bagaimana Cara Menghitung Kemiringan?

Kemiringan, yang sering disimbolkan dengan m, didefinisikan sebagai rasio perubahan vertikal ("Rise") terhadap perubahan horizontal ("Run") di antara dua titik mana pun pada garis.

Jika kita memiliki dua titik, Titik 1 (x₁, y₁) dan Titik 2 (x₂, y₂), rumusnya adalah:

m = (Perubahan y) / (Perubahan x) = (y₂ - y₁) / (x₂ - x₁)

Empat Jenis Kemiringan Garis

Arah dan nilai kemiringan memberi tahu kita karakteristik garis:

• Kemiringan Positif (+): Garis "naik" dari kiri ke kanan. (Saat x bertambah, y juga bertambah).
• Kemiringan Negatif (-): Garis "turun" dari kiri ke kanan. (Saat x bertambah, y berkurang).
• Kemiringan Nol (0): Garis horizontal (datar). (Perubahan y adalah 0).
• Kemiringan Tak Terdefinisi: Garis vertikal (tegak). (Perubahan x adalah 0, yang mengakibatkan pembagian dengan nol).

Visualisasi Interaktif

Gunakan applet GeoGebra berikut untuk menjelajahi konsep kemiringan. Coba gerakkan dua titik dan amati bagaimana "Rise" (Perubahan y) dan "Run" (Perubahan x) menentukan nilai kemiringan garis.

Menguasai konsep kemiringan sangat penting karena ini adalah dasar untuk memahami persamaan linear (y = mx + c), garis tegak lurus dan sejajar, dan pada akhirnya menjadi pengantar untuk konsep turunan (laju perubahan sesaat) dalam kalkulus.