Petualangan Bilangan: Faktor, Prima, & FPB
Panduan lengkap memahami struktur pembentuk angka, dari dasar hingga teknik lanjutan.
Pernahkah kamu ingin membagikan 20 permen jeruk dan 30 cokelat kepada teman-temanmu sehingga setiap orang mendapatkan jumlah yang sama rata tanpa ada sisa? Atau mungkin kamu ingin menyusun ubin lantai persegi agar pas menutupi ruangan tanpa perlu dipotong?
Kunci untuk memecahkan masalah kehidupan nyata ini adalah memahami Faktor dan FPB. Bukan hanya sekadar menghitung, tapi memahami bagaimana angka-angka "bekerja sama". Yuk, kita selidiki bersama!
1. Mengenal Faktor (Si "Pembentuk" Bilangan)
Bayangkan sebuah bilangan adalah sebuah bangunan. Faktor adalah batu bata penyusunnya. Secara matematika, faktor adalah bilangan bulat positif yang dapat membagi habis suatu bilangan tanpa menyisakan sisa (sisa = 0).
Setiap bilangan (kecuali 1) pasti memiliki setidaknya dua faktor, yaitu angka 1 dan bilangan itu sendiri. Namun, banyak bilangan memiliki teman faktor yang lebih banyak.
Contoh: Mencari Faktor dari Bilangan 10
Mari kita lakukan percobaan dengan membagi bilangan 10 dengan bilangan asli secara berurutan:
|
|
(Habis) → 1 adalah faktor. |
|
|
(Habis) → 2 adalah faktor. |
|
|
(Habis) → 5 adalah faktor. |
|
|
(Habis) → 10 adalah faktor. |
Jadi, faktor-faktor dari bilangan 10 adalah: 1, 2, 5, dan 10.
Konsep Pasangan Faktor: Faktor itu seringkali berpasangan! Untuk angka 10, pasangannya adalah (1 & 10) karena , dan (2 & 5) karena
.
2. Bilangan Prima & Komposit
Di dunia matematika, setiap bilangan memiliki "identitas" unik berdasarkan jumlah faktor yang dimilikinya. Ini adalah fondasi penting untuk matematika tingkat lanjut, seperti kriptografi (keamanan data).
| Jenis Bilangan | Definisi Lengkap | Contoh (Wajib Dihafal) |
|---|---|---|
| Bilangan Prima | Bilangan "eksklusif" yang hanya memiliki tepat 2 faktor: angka 1 dan dirinya sendiri. Mereka tidak bisa dibagi oleh angka lain. | 2, 3, 5, 7, 11, 13, 17, 19, 23... |
| Bilangan Komposit | Bilangan yang memiliki lebih dari 2 faktor (bisa dibagi angka lain selain 1 dan dirinya). | 4, 6, 8, 9, 10, 12, 14, 15... |
Alasannya: Bilangan 1 hanya memiliki 1 faktor saja (yaitu dirinya sendiri). Syarat prima harus 2 faktor, syarat komposit harus >2 faktor.
Apa itu Faktorisasi Prima?
Faktorisasi prima adalah proses memecah bilangan komposit menjadi perkalian bilangan-bilangan prima penyusunnya. Ini seperti mencari resep dasar atau "DNA" dari suatu angka.
Contoh Faktorisasi Prima bilangan 20:
3. Tiga Cara Mencari FPB (Faktor Persekutuan Terbesar)
FPB adalah bilangan bulat terbesar yang dapat membagi habis dua bilangan atau lebih secara bersamaan. Ada 3 metode utama untuk mencarinya. Pilihlah yang paling sesuai dengan soal yang kamu hadapi!
Cara 1: Mendaftar Faktor (Metode Visual)
Cara ini paling intuitif dan mudah dipahami. Sangat cocok untuk bilangan-bilangan yang kecil (misalnya di bawah 50).
Langkah: Daftar semua faktor dari kedua bilangan, lingkari angka yang muncul di kedua daftar, lalu pilih yang paling besar.
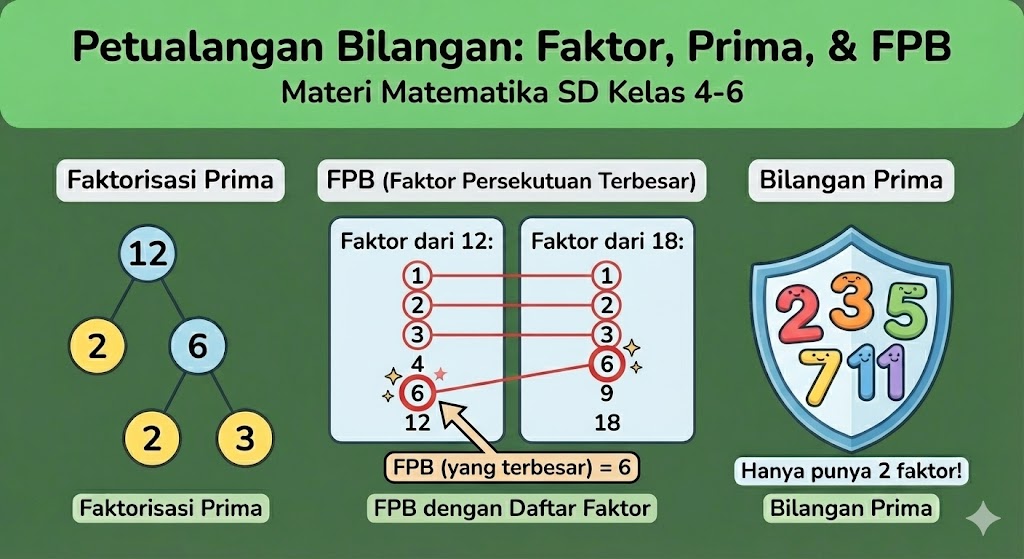
Contoh: Tentukan FPB dari 12 dan 18:
Faktor dari 12
Faktor dari 18
Faktor persekutuan (yang sama) adalah 1, 2, 3, dan 6. Yang terbesar adalah 6.
Cara 2: Pohon Faktor (Faktorisasi Prima)
Jika bilangannya ratusan atau ribuan, cara mendaftar akan terlalu lama dan rawan salah. Gunakan Pohon Faktor. Ini adalah metode standar yang sering dipakai di ujian sekolah.
1. Buat pohon faktor masing-masing bilangan.
2. Tuliskan perkalian faktorisasi primanya.
3. Kalikan faktor prima yang SAMA dengan pangkat TERKECIL.
Contoh: FPB dari 12 dan 18
Faktorisasi Prima 12:
Faktorisasi Prima 18:
Langkah Penyelesaian Langkah demi Langkah:
- Identifikasi yang SAMA: Cari faktor prima yang muncul di KEDUA bilangan. Di sini, angka 2 dan angka 3 muncul di kedua faktorisasi.
-
Pilih Pangkat TERKECIL: Bandingkan pangkatnya.
Analisis Faktor Prima 2:
Kita punya
(dari 12) dan
(dari 18).
Yang lebih kecil pangkatnya adalah 2 (atau
). Maka kita ambil 2.
Analisis Faktor Prima 3:Kita punya
(dari 12) dan
(dari 18).
Yang lebih kecil pangkatnya adalah 3. Maka kita ambil 3.
Tahukah kamu? Jika kamu sudah menemukan FPB dari dua bilangan (a dan b), kamu bisa mencari KPK-nya dengan rumus ajaib ini:
Cara 3: Algoritma Euclidean (Metode Pembagian Berulang)
Ini adalah metode "Detektif Matematika" yang ditemukan oleh matematikawan Yunani kuno bernama Euclid sekitar 300 SM. Cara ini sangat ampuh untuk mencari FPB dari bilangan yang sangat besar (misalnya ribuan) di mana membuat pohon faktor akan sangat melelahkan dan rentan salah.
Prinsipnya sederhana: FPB dari dua bilangan tidak akan berubah jika bilangan yang lebih besar dibagi dengan bilangan yang lebih kecil.
Caranya: Bagi bilangan besar dengan yang kecil. Ambil SISA pembagiannya. Lakukan terus menerus (pembagi lama dibagi sisa baru) sampai sisanya 0. Pembagi terakhir itulah FPB-nya.
Contoh Kasus: Mencari FPB dari 48 dan 18
Mari kita gunakan metode pembagian sisa ini:
-
Langkah 1: Bagi bilangan besar (48) dengan yang kecil (18).
dengan sisa 12.
-
Langkah 2: Geser! Sekarang bagi pembagi sebelumnya (18) dengan sisa tadi (12).
dengan sisa 6.
-
Langkah 3: Geser lagi! Bagi pembagi sebelumnya (12) dengan sisa tadi (6).
dengan sisa 0. (STOP!)
Karena sisanya sudah 0, kita lihat siapa pembagi terakhirnya? Pembagi terakhir adalah 6. Maka FPB-nya adalah 6.
4. Laboratorium Mini: Kalkulator Faktor
Ayo Bereksperimen!
Masukkan dua bilangan bulat positif (misal: 24 dan 36) untuk melihat faktor, FPB, dan jejak langkah Algoritma Euclidean secara instan.
Faktor Bilangan 1: ...
Faktor Bilangan 2: ...
Faktor Persekutuan: ...
FPB: ...
5. Tantangan Master Matematika
Siap untuk menguji kemampuanmu?
📚 Sumber & Referensi Belajar:
- Kemendikbud Ristek. (2022). Buku Panduan Guru & Siswa Matematika untuk SD/MI Kelas 4, 5, dan 6 (Kurikulum Merdeka). Jakarta: Pusat Perbukuan.
- Van de Walle, J. A., Karp, K. S., & Bay-Williams, J. M. (2019). Elementary and Middle School Mathematics: Teaching Developmentally. Pearson. (Buku standar internasional untuk pedagogi pengajaran konsep faktor dan bilangan).
- Khan Academy. Greatest Common Divisor & Euclidean Algorithm. (Penjelasan mendalam mengenai logika algoritma pembagian sisa).
- Wolfram MathWorld. Euclidean Algorithm Definition. (Definisi matematis formal untuk referensi lanjutan).