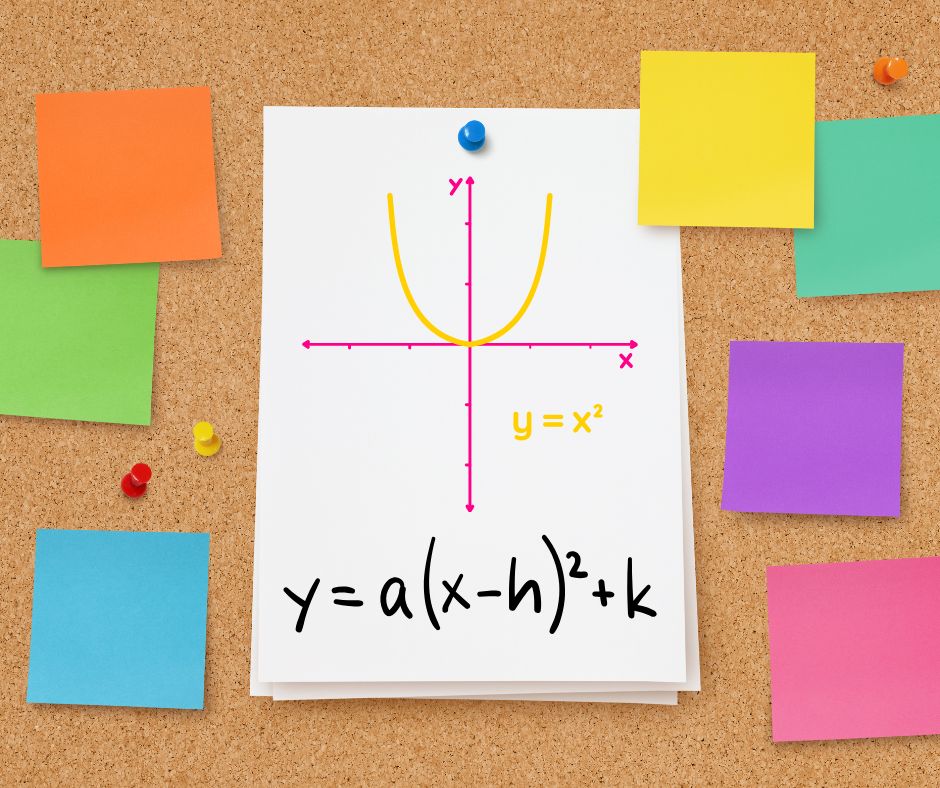Transformasi Grafik Fungsi Kuadrat: Memahami Peran a, h, dan k

Grafik fungsi kuadrat dasar, y = x², adalah parabola sederhana dengan titik puncak (vertex) di (0, 0). Namun, kita dapat memanipulasi grafik ini dengan mengubahnya ke Bentuk Puncak (Vertex Form):

y = a(x - h)² + k

Parameter a, h, dan k berfungsi sebagai "tombol kontrol" yang menggeser, meregangkan, memampatkan, dan membalik parabola dasar.

Membedah Parameter Transformasi

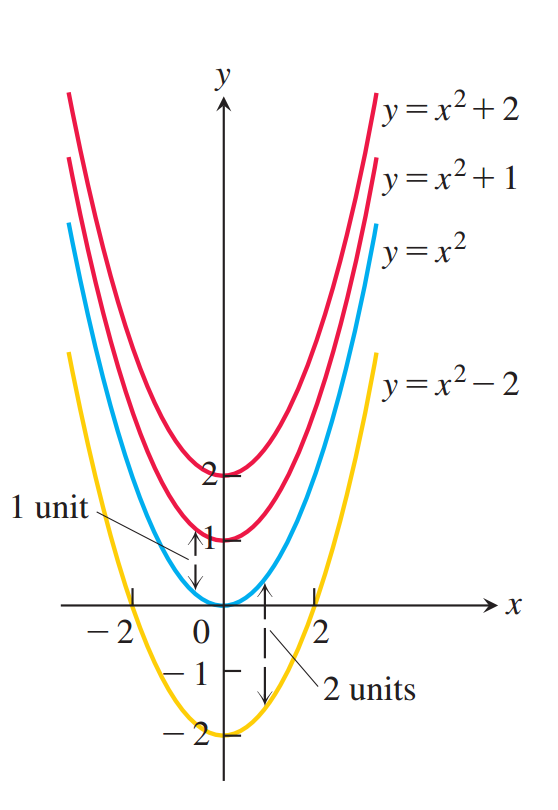
1. Pergeseran Vertikal (Parameter k)

Parameter k mengontrol pergeseran vertikal (naik/turun).

• Jika k > 0 (positif), grafik bergeser ke atas sejauh k unit.
• Jika k < 0 (negatif), grafik bergeser ke bawah sejauh k unit.

2. Pergeseran Horizontal (Parameter h)

Parameter h mengontrol pergeseran horizontal (kiri/kanan). Perhatikan tanda negatif dalam rumus.

• Jika bentuknya (x - 3)², maka h = 3, grafik bergeser ke kanan 3 unit.
• Jika bentuknya (x + 3)², ini sama dengan (x - (-3))², maka h = -3, grafik bergeser ke kiri 3 unit.

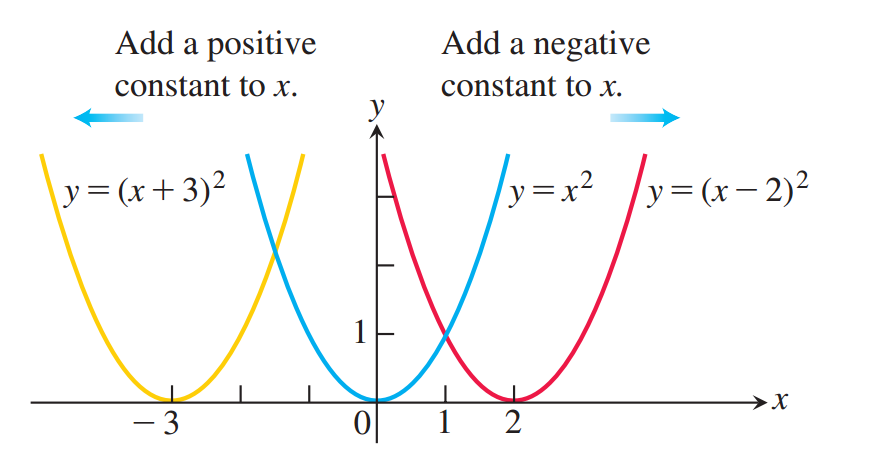
Titik puncak (vertex) baru dari parabola sekarang berada di titik (h, k).

3. Peregangan & Refleksi (Parameter a)

Parameter a mengontrol bentuk dan arah parabola.

• Jika a < 0 (negatif), parabola terbuka ke bawah (refleksi/pencerminan terhadap sumbu-x).
• Jika |a| > 1 (misal, a=2 atau a=-3), parabola mengalami peregangan vertikal (terlihat lebih "kurus").
• Jika 0 < |a| < 1 (misal, a=0.5 atau a=-0.2), parabola mengalami penyusutan vertikal (terlihat lebih "lebar").

Visualisasi Interaktif

Gunakan applet GeoGebra berikut untuk menjelajahi transformasi ini. Coba gerakkan slider a, h, dan k dan amati bagaimana masing-masing parameter memengaruhi bentuk dan lokasi grafik.